ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

Решение полученного уравнения или системы уравнений позволяет найти искомые величины.

В этой схеме содержится решение любой задачи на равноускоренное движение. Проиллюстрируем ее применение при решении еще одного примера.

Пример 4.2. Пуля, летящая со скоростью v₀, ударяет в земляной вал и, двигаясь внутри вала прямолинейно, проникает в него на глубину l. Сколько времени τ пуля двигалась внутри вала? С каким ускорением? На какой глубине скорость пули уменьшилась в n раз? Чему равна скорость пули к тому моменту, когда пуля пройдет m-ю часть своего пути внутри вала (l₁ = l / m)? Какой путь пройдет пуля за k-ю часть времени движения до остановки (t₁ = τ / k)? Движение пули считать равноускоренным.

Решение. Поскольку пуля двигалась равноускоренно, то для нее справедливы законы равноускоренного движения

(4.7)

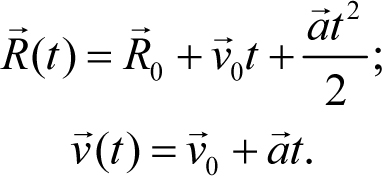
Начальным моментом для уравнений (4.7) будем считать момент влета пули в земляной вал.

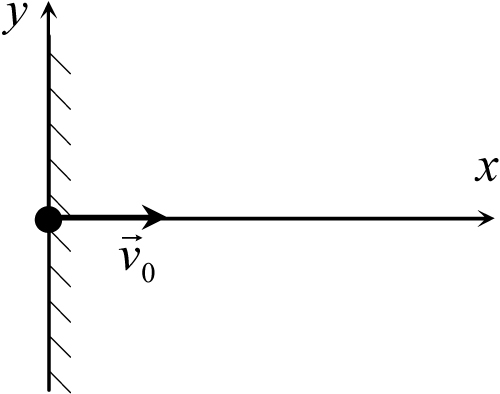
Перейдем теперь от векторных уравнений к уравнениям для проекций. Выберем систему координат так, как показано на рис. 4.6 и спроецируем уравнения (4.7) на ось x. Так как при нашем выборе системы координат ₀ = 0, (₀)_x = 0 получим

(4.8)

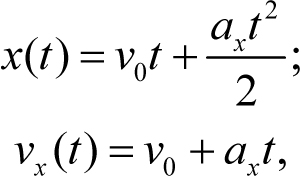
где a_x – проекция ускорения тела на ось x. Ускорение пули нам неизвестно, поэтому сначала нужно применить уравнения (4.8) к тем точкам траектории, информация о которых дана в условии, чтобы найти ускорение. Поэтому применим уравнения (4.8) к той точке, в которой пуля остановилась.