ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

То есть подставим в уравнения (4.8) неизвестное время движения до остановки τ. Тогда левые части уравнений (4.8) дадут координату этой точки и проекцию скорости пули в ней на ось x. Поскольку при нашем выборе системы координат координата точки остановки равна тому расстоянию, которое пуля прошла внутри вала, то есть l, а скорость пули в ней равна нулю, то

(4.9)

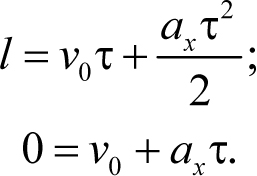
Система двух уравнений (4.9) содержит две неизвестные величины a_x и τ, и, следовательно, может быть решена. Выражая из второго уравнения время τ

(4.10)

и подставляя его в первое уравнение системы (4.9), найдем проекцию ускорения пули

(4.11)

а затем из уравнения (4.10) – полное время движения

(4.12)

Из соотношения (4.11) видим, что проекция ускорения на ось x оказалась отрицательной, т. е. вектор ускорения направлен против оси x, то есть против движения пули. Этот результат можно было ожидать заранее: в процессе движения внутри вала пуля тормозилась, поэтому вектор изменения скорости за любой интервал времени, а следовательно, и вектор ускорения пули направлен противоположно выбранной оси x, поэтому a_x < 0.

Найдем теперь глубину, на которой скорость пули уменьшилась в n раз. Для этого применим уравнения движения (4.8) к этой точке, т. е. подставим в них время движения до этой точки τ₁ (оно нам пока не известно) где a – модуль вектора ускорения пули.