ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
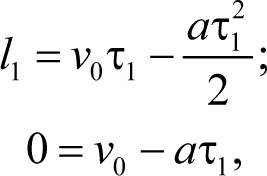
Левая часть второго уравнения движения в момент τ1 дает v0 / n, первого – неизвестную координату исследуемой точки, которая при нашем выборе системы координат равна расстоянию от этой точки до точки влета пули в земляной вал (оно обозначено в первом уравнении (4.13) как l1). Выражая время τ1 из второго уравнения 
, подставляя его в первое и используя формулу для ускорения (4.11), найдем
Теперь найдем скорость пули в точке, находящейся на расстоянии l / m от начала координат. Для этого применим уравнения (4.8) к этой точке. То есть подставим в уравнения (4.8) время движения до этой точки τ2. Поскольку при нашем выборе системы координат координата пули в ней равна l / m, то
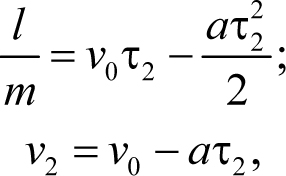
где v2 – скорость пули в рассматриваемой точке. Из первого уравнения (4.15) найдем время τ2
Оба корня (4.16) положительны, и, значит, определяют два момента времени, когда пуля находилось на глубине l / m. С другой стороны, очевидно, что пуля находилось в этой точке один раз. Почему же первое уравнение (4.15) имеет два корня? Это связано с тем, что движение пули является равноускоренным только до момента остановки, и, следовательно, уравнения (4.7) справедливы только до этого момента. Если бы уравнения (4.7) были бы справедливы при любых t > 0, то после остановки пуля начала бы двигаться назад, разгоняясь, и второй раз прошла бы точку l / m, чего, конечно, не будет.
