ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Как обсуждалось в предыдущей главе, при свободном движении тела вблизи поверхности земли (т.е. в отсутствие других сил, кроме силы тяжести) его ускорение одинаково в каждой точке траектории и не зависит от массы тела. Направлен вектор ускорения тел вертикально вниз и равен по величине 9,8 м/с2 (ускорение свободного падения) (см. также предыдущую главу). Поэтому такое движение является равноускоренным, и, следовательно, зависимости радиусвектора тела по отношению к произвольной системе координат 
(t) и его скорости 
(t) от времени определяются законами равноускоренного движения, которые использовались и в предыдущей главе
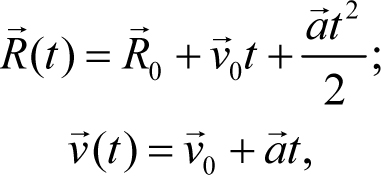
где 0 и 0 – радиус-вектор и скорость тела в начальный момент времени t = 0, 
= 
– ускорение свободного падения. Главное свойство уравнений (5.1) заключается в том, что они представляют собой зависимости координат от времени, и что время t в этих уравнениях – это не полное время движения или время движения до верхней точки траектории. Время t в уравнениях (5.1) – переменная величина. Это значит, что мы можем подставлять в уравнния (5.1) любые значения времени (отсчитанные от момента t = 0) и находить с помощью этих уравнений радиус-вектор и скорость тела в этот момент времени. При этом для нахождения тех или иных характеристик движения из уравнений (5.1), как правило, удобнее проецировать векторные уравнения (5.1) на координатные оси, а затем использовать числовые зависимости координат тела и проекций его скорости на эти оси от времени.
Из уравнений (5.1) следует, что равноускоренное движение будет прямолинейным, если векторы начальной скорости и ускорения направлены одинаково или противоположно (поскольку согласно (5.1) все характеристики движения выражаются через эти векторы).
