ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Если же векторы начальной скорости и ускорения направлены под ненулевым углом друг к другу – равноускоренное движение будет криволинейным (как при броске тела под углом к горизонту). Технически рассмотрение движения под углом к горизонту отличается рассмотрения прямолинейного движения тем, что здесь необходимо использовать две координатных оси (а не одну как при прямолинейном движении). Все остальные принципы рассмотрения криволинейного движения – точно такие же. Рассмотрим пример.
Пример 5.1. Тело бросили с поверхности земли с начальной скоростью ![]() 0, направленной под углом α к горизонту. Найти: максимальную высоту подъема тела над поверхностью, время подъема на эту высоту, время, через которое тело упадет на землю, расстояние от точки бросания до точки падения, скорость, которую будет иметь тело перед самым падением на землю, угол подлета тела к поверхности земли.
0, направленной под углом α к горизонту. Найти: максимальную высоту подъема тела над поверхностью, время подъема на эту высоту, время, через которое тело упадет на землю, расстояние от точки бросания до точки падения, скорость, которую будет иметь тело перед самым падением на землю, угол подлета тела к поверхности земли.
Решение. Поскольку движение тела равноускоренное, зависимости его радиус-вектора ![]() (t) и скорости
(t) и скорости ![]() (t) от времени определяются уравнениями (5.1). Проецируя эти векторные уравнения на оси x и y (рис. 5.1), получим
(t) от времени определяются уравнениями (5.1). Проецируя эти векторные уравнения на оси x и y (рис. 5.1), получим
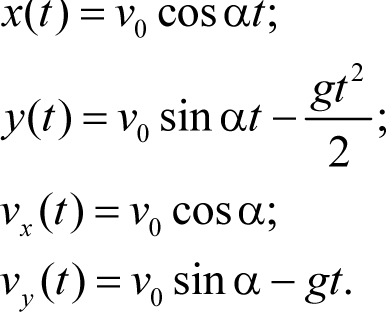
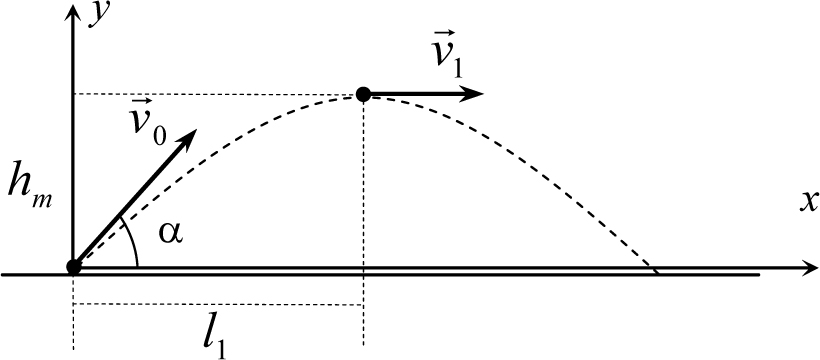
Рис. 5.1


