ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Тогда первое из уравнений (5.2) даст x координату точки падения (при нашем выборе системы координат эта величина совпадает с дальностью полета тела), последнее – проекцию вектора скорости тела в момент падения на ось y. Второе уравнение системы (5.2) в применении к точке падения даст нам y-координату точки падения, которая при нашем выборе системы координат равна нулю:
Решая квадратное уравнение (5.5), найдем два значения полного времени движения t2
Очевидно, первый из этих корней отвечает началу движения, поскольку условие (5.5) отвечает, фактически, не конечной точке траектории, а точке с y-координатой, равной нулю, то есть и начальной, и конечной точкам. Поэтому полное время движения определяется вторым корнем (5.6). Подставляя это время в остальные уравнения, найдем дальность полета тела l и проекцию его скорости на вертикальную ось в момент падения vy(t2)
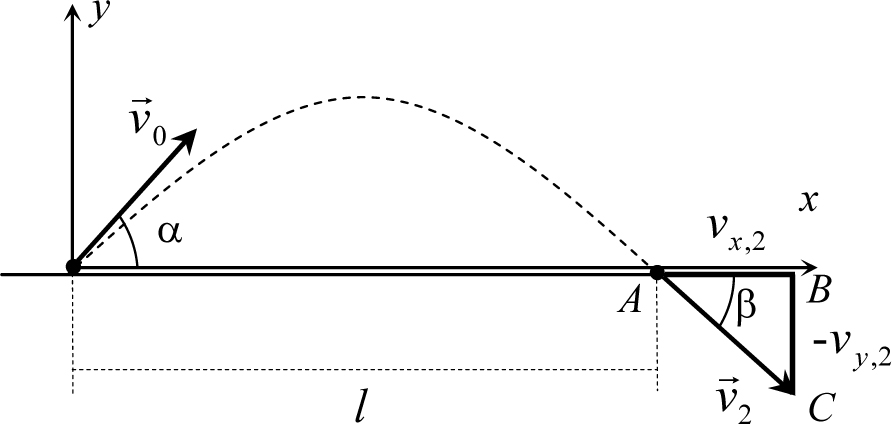
Рис. 5.2
Проекция конечной скорости тела на ось y оказалась отрицательной, как это и должно быть, поскольку угол между вектором конечной скорости и осью y тупой (рис. 5.2).


