ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Из второй формулы (5.7) и третьего из уравнений (5.2) найдем величину конечной скорости тела v2:
Угол подлета тела к земле – это угол между вектором скорости тела и поверхностью земли. Этот угол можно найти из треугольника, гипотенузой которого является вектор скорости, катетами – его проекции на горизонтальную и вертикальную оси (треугольник АВС, см. рис. 5.2). Имеем
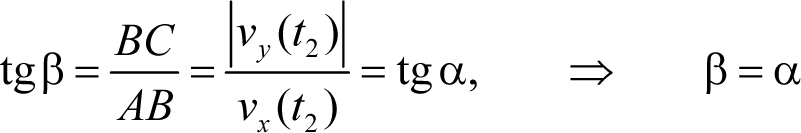
(модуль от проекции vy(t2) мы взяли потому, что эта проекция отрицательна).
Из полученных соотношений следует, что: (а) полное время движения вдвое больше времени подъема на максимальную высоту (и, следовательно, время подъема равно времени спуска), (б) конечная скорость равна начальной, (в) угол падения равен углу бросания. При этом эти результаты получались «сами» из уравнений движения, то есть их не пришлось предполагать заранее.
Отметим также, что при фиксированной величине начальной скорости дальность полета тела максимальна, если sin 2α = 1 (см. первое из соотношений (5.7)), или α = 45°. При этом сама максимальная дальность полета тела равна
![]()
Важной особенностью описания равноускоренного криволинейного движения является возможность представить его как совокупность двух движений: равномерного в направлении, перпендикулярном ускорению, и равноускоренного в направлении ускорения (эту особенность первым понял Г. Галилей). Действительно, уравнения движения, которые получаются в результате проецирования уравнений (5.1) на перпендикулярную и параллельную ускорению оси оказываются такими же, как для равномерно и равноускоренно движущегося тела. Такая возможность позволяет значительно упростить анализ уравнений движения. В качестве примера рассмотрим следующую задачу.


