ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
где Δvx = vx(t + Δt) − vx(t) – проекция вектора изменения (или приращения) скорости тела за малый интервал времени Δt, взятый около момента t, на ось x. Все величины, входящие в соотношение (6.1) имеют графический образ на графике vx(t).
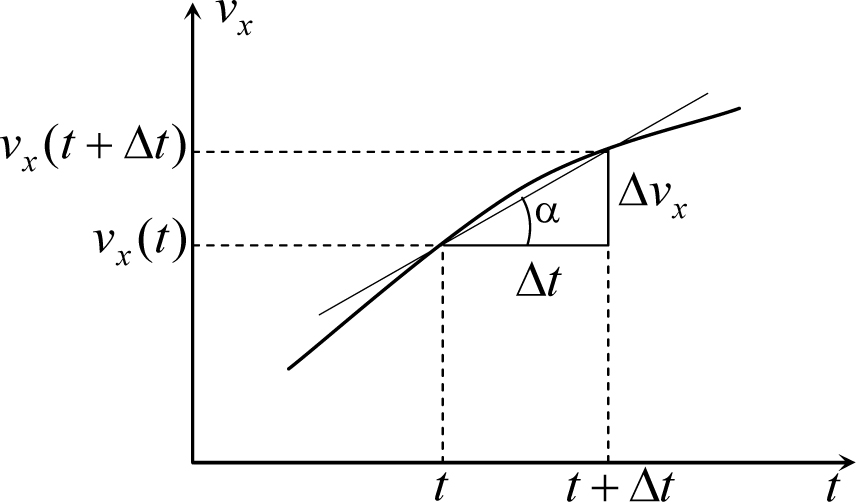
Рис. 6.2
Интервалу времени Δt отвечает отрезок на оси времени длиной Δt в том масштабе, который принят для оси времени. Разности проекций скорости vx(t + Δt) − vx(t) отвечает отрезок оси vx (в соответствующем масштабе) около значения скорости vx(t) (рис. 6.2). Поэтому отношение (6.1) представляет собой тангенс угла наклона секущей к графику vx(t), проведенной около момента времени t. При устремлении Δt к нулю (именно этот предельный переход необходимо осуществить в (6.1) для нахождения мгновенного ускорения) секущая превращается в касательную, и, следовательно, проекция мгновенного ускорения тела в некоторый момент времени равна тангенсу угла между касательной к графику зависимости проекции скорости тела от времени в этот момент и осью времени. Если считать углы, отсчитанные от оси времени против часовой стрелке положительными, по - отрицательными (так же как в тригонометрии), то это соотношение имеет алгебраический смысл (со знаком).
Как следует из рис. 6.1, углы между касательными к графику в моменты времени t1 и t2 и осью времени приблизительно одинаковы по величине, но отсчитаны против и по часовой стрелке соответственно.


