ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Поэтому величина ускорения тела в эти моменты одинакова, но в момент времени t1 проекция ускорения на ось x отрицательна (то есть вектор ![]() в этот момент направлен против оси x), в момент t2 положительна (а вектор ускорения в этот момент направлен вдоль оси x). Модуль вектора ускорения тела в момент времени t3 больше ускорения при t = t1 и t = t2, а направлен вектор ускорения тела в этот момент в положительном направлении оси x.
в этот момент направлен против оси x), в момент t2 положительна (а вектор ускорения в этот момент направлен вдоль оси x). Модуль вектора ускорения тела в момент времени t3 больше ускорения при t = t1 и t = t2, а направлен вектор ускорения тела в этот момент в положительном направлении оси x.
Соотношение (6.1) и логика предельного перехода Δt → 0 совпадают с определением производной функции. Отсюда заключаем, что мгновенное ускорение тела есть производная зависимости скорости от времени.
Аналогичные рассуждения проводятся при исследовании геометрического смысла производной, поэтому мгновенное ускорение (6.1) представляет собой производную скорости по времени.
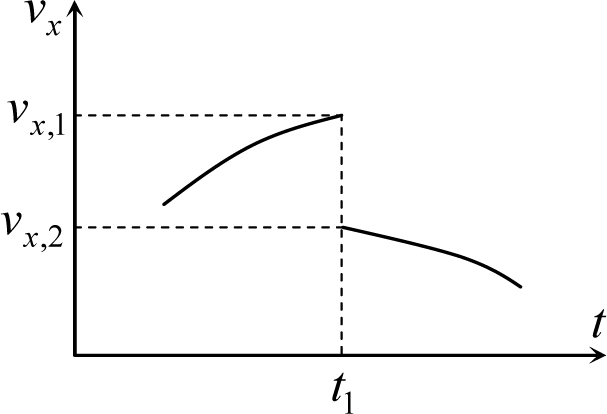
Рис. 6.3


