ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
По графику зависимости скорости от времени можно находить не только ускорение тела, но и его положение в пространстве в любой момент времени, и в частности, пройденные телом за те или иные интервалы времени пути.
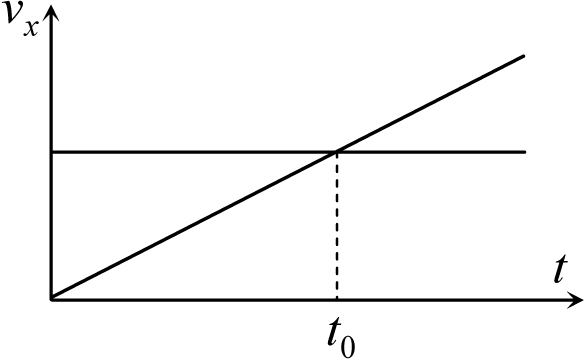
Рис. 6.4
Пример 6.2. Два тела движутся из одной точки вдоль одной оси x. Даны графики зависимости проекций скоростей тел на эту ось от времени. Через какое время тела встретятся? Момент t0 задан (рис. 6.4).
Решение. Докажем, что изменение координаты тела по некоторой оси x за интервал времени от некоторого момента tн до некоторого момента tк равно площади фигуры на графике зависимости проекции скорости на ось x от времени, ограниченной графиком vx(t), осью времени и вертикальными прямыми t = tн и t = tк.
Для доказательства возьмем определение мгновенной скорости тела
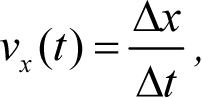 где Δt – бесконечно малый интервал времени около момента t, Δx – изменение координаты тела за этот интервал времени. Из определения (6.3) находим изменение координаты тела Δx за бесконечно малый интервал времени Δt около момента времени t
где Δt – бесконечно малый интервал времени около момента t, Δx – изменение координаты тела за этот интервал времени. Из определения (6.3) находим изменение координаты тела Δx за бесконечно малый интервал времени Δt около момента времени t
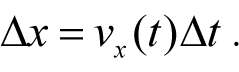 Изменение координаты тела за конечный интервал времени от момента tн до момента tк равно сумме изменений координаты за бесконечно малые интервалы Δt1, Δt2, Δt3, ..., на которые можно разделить весь интервал tк − tн:
Изменение координаты тела за конечный интервал времени от момента tн до момента tк равно сумме изменений координаты за бесконечно малые интервалы Δt1, Δt2, Δt3, ..., на которые можно разделить весь интервал tк − tн:
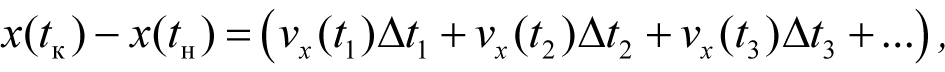 где vx(t1), vx(t2), vx(t3), ... – значения проекции скорости тела на первом, втором, третьем и т.д. бесконечно малых интервалах
где vx(t1), vx(t2), vx(t3), ... – значения проекции скорости тела на первом, втором, третьем и т.д. бесконечно малых интервалах
(6.3)
(6.4)


