ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ

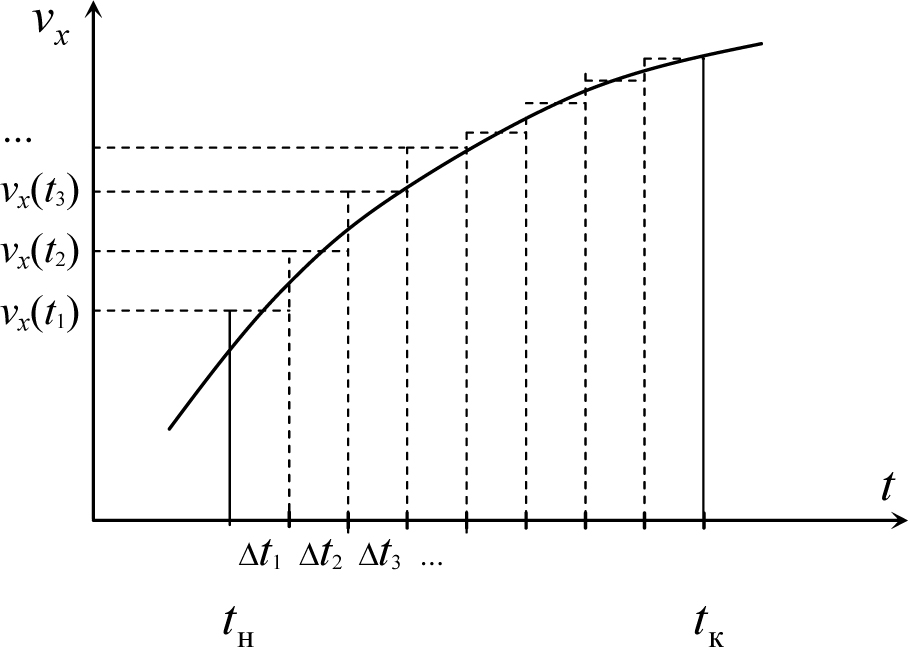
Δt₁, Δt₂, Δt₃, ... Сумма (6.4) содержит бесконечное количество слагаемых, поэтому ее вычисление, как правило, представляет собой сложную математическую проблему, для решения которой необходима высшая математика. Однако эта сумма имеет простой графический смысл (рис. 6.5).

Действительно, все входящие в выражение (6.4) величины имеют следующий графический образ на графике v_x(t). Бесконечно малые интервалы времени Δt_i можно отложить на оси времени (в том масштабе, который принят для этой оси). Значения скорости тела на этих интервалах времени равны длинам отрезков, соединяющих ось времени и график функции, и перпендикулярных оси времени (в соответствующем масштабе). Поэтому каждое слагаемое, входящее в сумму (6.4) представляет собой площадь узкого прямоугольника, основанием которого является интервал времени Δt_i, высотой – значение скорости в какой-то точке внутри этого интервала v_x(t_i). Поэтому сумма (6.4) равна площади ступенчатой фигуры, а при уменьшении интервалов времени – площади фигуры, ограниченной графиком функции v_x(t) и вертикальными отрезками t = t_н и t = t_к.

Из доказанного утверждения сразу следует ответ на вопрос задачи.