ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Так как начальные координаты тел равны, то их координаты снова будут совпадать в такой момент времени t1, что площади под двумя графиками от t = 0 до t1 = t равны. Очевидно, это момент 2t0. Действительно, площади прямоугольного треугольника и прямоугольника с одинаковыми основаниями равны, если высота треугольника вдвое больше высоты прямоугольника. Таким образом, тела снова встретятся через время 2t0 после начала движения.
В заключение отметим следующее важное обстоятельство. Проекция скорости на ось x может быть как положительной, так и отрицательной. Поэтому в сумму (6.4) могут входить как положительные, так и отрицательные слагаемые. Следовательно, изменение координаты тела за некоторый конечный интервал времени равно «алгебраической» площади под графиком функции vx(t), в которую участки графика с положительной проекцией vx(t) дают положительные вклады, с отрицательной проекцией vx(t) – отрицательные (т. е. площадь для таких участков нужно считать отрицательной). Если же мы хотим найти пройденный телом путь, то в формуле (6.4) следует модуль проекции скорости, а площади под графиком скорости нужно считать положительными независимо от знака проекции скорости.
С помощью графиков можно установить и обратную связь, то есть определять скорость тела по зависимости его координаты от времени. Рассмотрим пример такого рода.
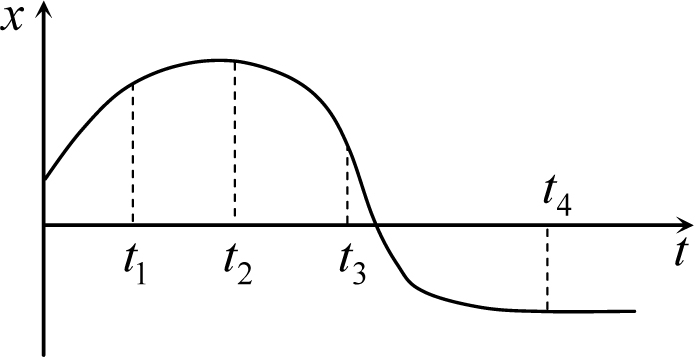
Рис. 6.6
Пример 5.3. Тело движется прямолинейно вдоль некоторой оси x. Дан график зависимости x-координаты тела от времени (рис. 6.6). Сравнить проекции скорости тела на ось x в моменты времени t1, t2, t3 и t4. Доказать, что на графике x(t) не может быть разрывов и изломов.
Решение. Поскольку связь между координатой и проекцией скорости такая же, как между проекциями скорости и ускорения, то для нахождения проекции скорости по графику координаты можно применить тот же прием, что был использован для нахождения ускорения по скорости.


