ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
А именно, проекция скорости тела в некоторый момент времени равна тангенсу угла между касательной к графику x(t) в этот момент времени и осью времени. Причем для этих углов применяется такое же правило знаков, как в тригонометрии. Угол, отсчитанный от оси времени против часовой стрелки считается положительным (и имеет положительный тангенс), по часовой стрелке – отрицательным (с отрицательным тангенсом). Поэтому из данного в условии графика следует, что величина скорости тела в моменты времени t2 и t4 меньше величины скорости в моменты t1 и t3, причем vx(t3) отрицательна, vx(t1) положительна и |vx(t3)| > |vx(t1)|.
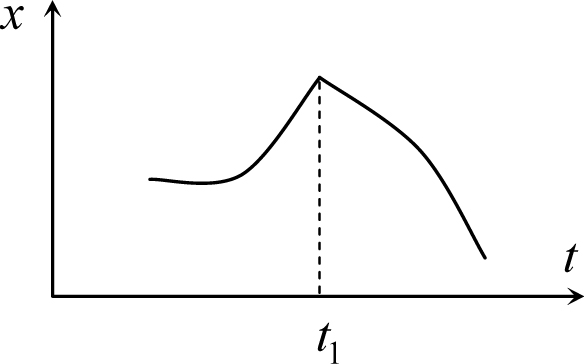
Рис. 6.7
Из этих рассуждений следует, что существование излома на графике координаты (пример излома графика приведен на рис. 6.7) аналогично существованию разрыва на графике скорости. Действительно, если бы излом существовал, то наклон касательной к графику слева и справа от момента излома был разным (причем бесконечно близко к этому моменту). Поэтому скорость тела в этот момент изменялась бы на конечную величину за бесконечно малый интервал времени, то есть зависимость проекции скорости тела от времени имела бы в этот момент разрыв. А поскольку это означало бы бесконечно большое ускорение (см. пример 6.1), то изломов на графике координаты быть не может (см., однако, пример 6.5).
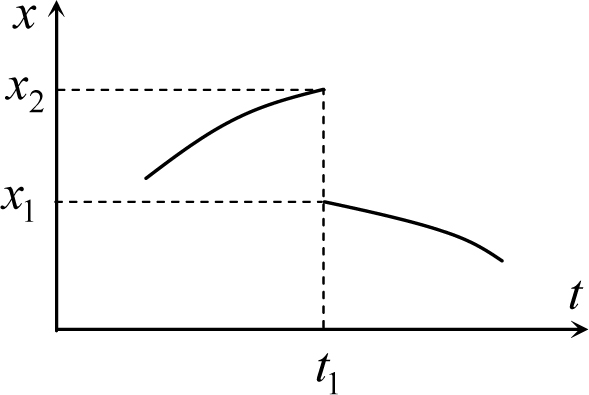
Рис. 6.8
Что касается разрывов, то их отсутствие на графике зависимости координаты от времени очевидно. Действительно, если бы такой разрыв существовал, это означало бы, что за бесконечно малый интервал времени вблизи времени, отвечающей точке разрыва (t1 на рис. 6.8) координата тела менялась на конечную величину Δx = x2 − x1 (см. рис. 6.8).


