ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Поэтому мгновенная скорость тела в момент времени t1 стремилась бы к бесконечности
поскольку числитель формулы (6.5) не стремится к нулю при стремлении к нулю знаменателя. А поскольку бесконечной скорости быть не может, то и не может быть разрывов на графике зависимости скорости от времени.
Наиболее распространенными задачами на графики движений, входящими в школьный курс физики, являются задачи на «перестроение» графиков движений из одних координат в другие. Например, дается график зависимости скорости тела от времени, а требуется построить график зависимости координаты или ускорения от времени. При этом, как правило, рассматривается равноускоренное движение, но состоящее из нескольких этапов с разным ускорением на каждом. Как показывает опыт приема вступительных экзаменов или проведения олимпиад по физике, основной трудностью в этих задачах является не построение правильного графика на каждом этапе, а правильное «сопряжение» графиков на разных этапах. Рассмотрим характерный пример.
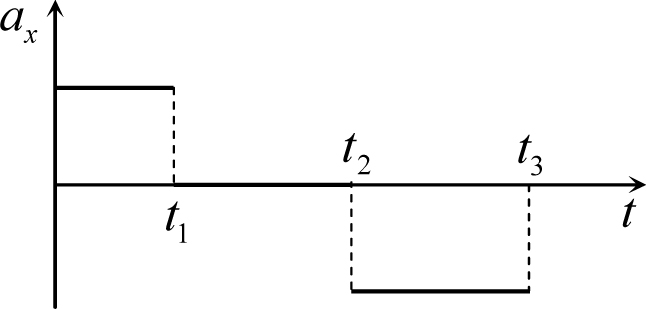
Рис. 6.9
Пример 6.4. Тело движется прямолинейно вдоль некоторой оси. Дан график зависимости проекции ускорения тела на эту ось от времени (рис. 6.9). Построить графики зависимости координаты тела и проекции его скорости на эту ось от времени. Начальную координату и проекцию начальной скорости тела взять равными нулю.
Решение. Поскольку ускорение тела внутри каждого из интервалов времени − t1, t1 − t2 и t2 − t3 не изменяется, то внутри каждого интервала движение тела является равноускоренным. Поэтому внутри каждого из перечисленных интервалов зависимость координаты тела и его скорости от времени определяется законами равноускоренного движения с разными ускорениями (причем одно из них – от t1 до t2 – равно нулю, поэтому движение тела в этом интервале времени является равномерным).


