ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Кроме того, очевидно, что начальная координата и начальная скорость тела на каждом интервале времени совпадают с конечными значениями этих величин на предыдущем интервале. Поэтому если бы мы «честно» вычисляли конечные значения координаты и скорости тела на каждом интервале и использовали эти величины для построения графика на «следующем», то все получилось бы правильно само собой. Однако задача здесь стоит по-другому: нужно не проводя конкретных вычислений, а используя свойства законов равноускоренного движения качественно построить требуемые графики, правильно уловив их характерные особенности (возрастаниеубывание, наклоны, наличие экстремумов и т.д.). При этом графики на разных этапах движения должны правильно сопрягаться друг с другом.
Рассмотрим сначала участок графика от момента времени t = 0 до t = t1. Поскольку движение тела внутри этого интервала времени является равноускоренным, то зависимости проекции скорости тела на ось x и его x-координаты от времени даются уравнениями равноускоренного движения
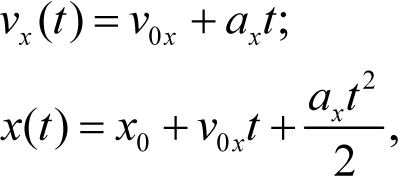 где x0 и v0x – координата тела и проекция его скорости на ось x в момент времени t = 0, ax – проекция ускорения, которая, как это следует из данного в условии графика, положительна. Величины x0 и v0x никак не определяются из данного в условии графика и потому должны быть даны дополнительно. В соответствии с условием возьмем эти величины равными нулю: x0 = 0, v0x = 0 . Тогда зависимости (6.6) будут иметь вид
где x0 и v0x – координата тела и проекция его скорости на ось x в момент времени t = 0, ax – проекция ускорения, которая, как это следует из данного в условии графика, положительна. Величины x0 и v0x никак не определяются из данного в условии графика и потому должны быть даны дополнительно. В соответствии с условием возьмем эти величины равными нулю: x0 = 0, v0x = 0 . Тогда зависимости (6.6) будут иметь вид
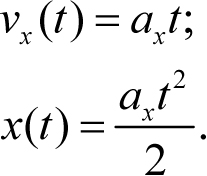 Этим зависимостям отвечают на графиках vx(t) и x(t) прямая, проходящая через начало координат, и парабола, с ветвями, направленными вверх, вершина которой находится в начале координат (см. графики на интервалах 0 − t1 на рис. 6.10 и 6.11).
Этим зависимостям отвечают на графиках vx(t) и x(t) прямая, проходящая через начало координат, и парабола, с ветвями, направленными вверх, вершина которой находится в начале координат (см. графики на интервалах 0 − t1 на рис. 6.10 и 6.11).
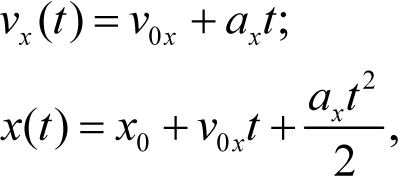
(6.6)
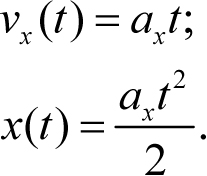
(6.7)


