ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
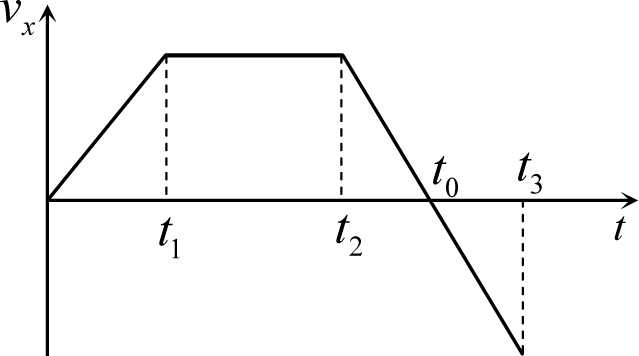
Рис. 6.10
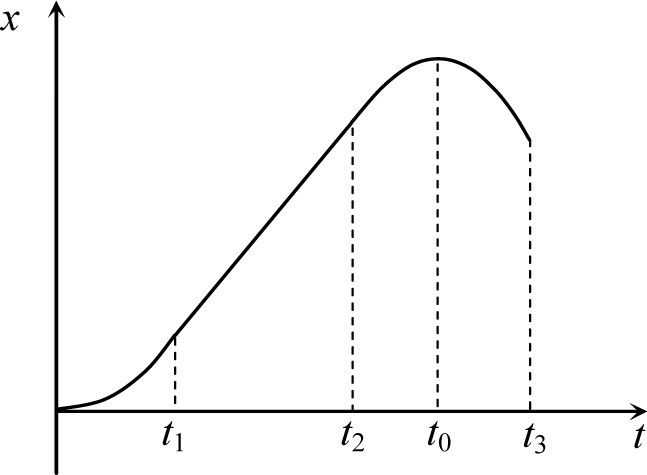
Рис. 6.11
Второй интервал времени t1 − t2. Поскольку ускорение тела в этом интервале равно нулю, то движение тела здесь равномерное. Поэтому скорость тела внутри этого интервала не изменяется, а зависимость координаты от времени является линейной функцией. Кроме того, график зависимости скорости от времени не должен иметь разрывов, а координаты – разрывов и изломов (см. предыдущие примеры). Следовательно, этот участок на графике скорости изображается горизонтальной прямой, расположенной на той же «высоте», на которой закончился график на первом участке, на графике координаты – наклонной прямой, сопрягающейся с предыдущим участком без излома (см. соответствующие участки графиков на рис. 6.10. и 6.11).
Интервал времени t2 − t3. На этом участке движение тела равноускоренное, поэтому проекция скорости является линейной, а координата - квадратичной функцией времени. На графиках vx(t) и x(t) им отвечают соответственно прямая линия и квадратичная парабола. Так как проекция ускорения тела на этом участке отрицательна, а величина ускорения приблизительно такая же как на участке 0 − t1 (это следует из данного в условии рисунка), то прямая на графике скорости должна быть убывающей с тем же наклоном, что и прямая на участке 0 − t1, ветви параболы на графике координаты вниз с тем же «расстоянием» между ветвями, что и у параболы на участке 0 − t1.


