Вариант 1: Работа с циклическим списком

Необходимо написать программу, которая реализует хранение и простейший набор функций для обработки данных о некоторых объектах нашего бренного мира, выбираемых по вариантам (будут приведены ниже).

Каждый элемент должен представлять собой структуру данных с необходимым набором полей, а все элементы должны представлять собой циклический список (односвязный или двусвязный – решайте сами). В программе должно быть меню, позволяющее выполнить следующие действия:

1. Добавить элемент

2. Удалить элемент

3. Вывести элементы на экран

4. Выйти

При добавлении элемента необходимо спросить у пользователя значения всех необходимых полей структуры, заполнить ими структуру, и добавить её в список (в любое место какое нравится).

При удалении элемента необходимо спросить у пользователя, по значению какого поля структуры необходимо выполнить удаление и, если таких элементов несколько, удалить их все. Номер варианта выбирается следующим образом: берёте свой номер по журналу, находите остаток от его деления на 5 и прибавляете 1.

Структуры данных для хранения:

Вариант 1: Фамилия студента, имя студента, коэффициент IQ

Вариант 2: Фамилия автора, название книги, год выпуска

Вариант 3: Название страны, площадь, население

Вариант 4: Марка автомобиля, масса, стоимость

Вариант 5: Название небесного тела, масса, первая космическая скорость.

Вариант 2: Работа с двоичным деревом поиска

В рамках работы необходимо построить двоичное дерево поиска,

вывести его как-то красиво на экран (сами придумайте как, но без

фанатизма) и реализовать поиск значений, которые есть в его узлах.

Значениями в рамках работы следует сделать обычные целые числа.

Двоичное дерево поиска – двоичное дерево, для которого

выполняются следующие дополнительные условия (свойства дерева поиска):

1. оба поддерева — левое и правое — являются двоичными деревьями

поиска;

2. у всех узлов левого поддерева произвольного узла X значения

ключей данных меньше либо равны, нежели значение ключа данных самого

узла X;

3. у всех узлов правого поддерева произвольного узла X значения

ключей данных больше, нежели значение ключа данных самого узла X.

Пример двоичного дерева:

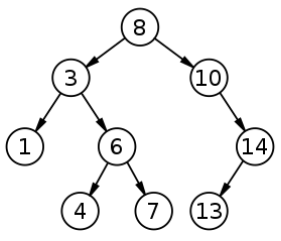
Количество вершин в дереве следует задать с помощью define-константы, на этапе тестирования можно его установить, например, в значение 7. Целые числа в вершинах дерева можно или считать из файла, имя которого потребовать задать в аргументах командной строки, или сгенерировать случайными.

Дерево должно быть реализовано в программе с помощью двусвязного списка, каждый узел которого будет содержать 3 поля: указатель на левое поддерево, информационное поле (в нём будет храниться выводимое целое число), указатель на правое поддерево.

После построения дерева и вывода его на экран пользователю необходимо предоставить возможность выполнять поиск элементов в дереве по значению их информационной части (целого числа). Задача поиска – сообщить, присутствует ли введённое значение в дереве или нет.

Неподготовленным умам задача может показаться сложной, но в действительности ничего сложного в её реализации нет. По сути дела, для выполнения этой работы вам необходимо будет сделать следующее:

1. Сгенерировать (или считать из файла) заданное константой количество случайных чисел. Если это количество 7, то, допустим, они у вас следующие: 6, 2, 8, 4, 9, 5, 1

2. Объявить структуру данных для узла дерева

3. Построить из сгенерированных чисел двоичное дерево поиска. Это делается весьма просто: для каждого нового числа нужно начиная с корня дерева спускаться вниз до тех пор, пока не обнаружите отсутствие узла. Как только обнаружили – вставляете в это место дерева новый узел с указанным числом в информационной части. Для приведённых выше чисел это дерево будет следующим:

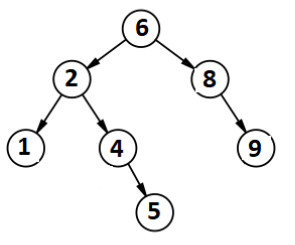
Получилось оно именно таким следующим образом:

а. Первую вершину делаем корнем, без вариантов

б. Для второй вершины (со значением 2) смотрим, начиная от корневой вершины, больше или меньше её значение, чем значение в вершине. 2 меньше 6, поэтому добавляем вершину в левое поддерево. 

в. Следующее число – 8. Опять смотрим, начиная с корня. Понимаем, что 8 больше чем 6, поэтому добавляем её вправо от корня.

г. Следующее число – 4. Опять смотрим, начиная с корня. 4 меньше чем 6, поэтому переходим к правому поддереву корня, но там у нас уже есть вершина со значением 2. Сравниваем число в добавляемой вершиной со значением в вершине 2, понимаем, что 4 больше 2, значит добавляем вершину со значением 4 справа от 2.

д. И так далее.

4. Вывести на экран построенное дерево (если вам кажется, что выводить на экран готовое дерево слишком сложно, вывод на экран можно делать в процессе построения, так будет немного проще)

5. Предложить пользователю ввести число, после чего сообщить, есть ли такое число в дереве.