Спектральная плотность продифференцированного сигнала

Пусть сиг­нал u(t) и его спек­траль­ная плот­ность S(jω) за­да­ны. По­да­дим сиг­нал на вход ли­ней­но­го устрой­ства, осу­ществ­ля­ю­ще­го диф­фе­рен­ци­ро­ва­ние сиг­на­ла. Сиг­нал на вы­хо­де диф­фе­рен­ци­ру­ю­ще­го устрой­ства бу­дет иметь вид:

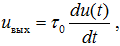
где τ₀ — кон­стан­та пре­об­ра­зо­ва­ния.

Ис­поль­зуя свой­ство пре­об­ра­зо­ва­ния Фу­рье, ча­сто за­пи­сы­ва­е­мое в ви­де:

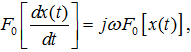
где сим­во­лом F(₀ обо­зна­че­но пря­мое пре­об­ра­зо­ва­ние Фу­рье над функ­ци­ей x(t),по­лу­чим:

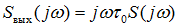
Итак, диф­фе­рен­ци­ро­ва­ние сиг­на­ла по вре­ме­ни эк­ви­ва­лент­но ал­геб­ра­и­че­ской опе­ра­ции умно­же­ния спек­траль­ной плот­но­сти на мно­жи­тель jω, ча­сто на­зы­ва­е­мым опе­ра­то­ром диф­фе­рен­ци­ро­ва­ния в ча­стот­ной об­ла­сти. От­ме­тим, что при диф­фе­рен­ци­ро­ва­нии ско­рость из­ме­не­ния сиг­на­ла во вре­ме­ни воз­рас­та­ет, а сам сиг­нал уко­ра­чи­ва­ет­ся. Сле­до­ва­тель­но, мо­дуль спек­тра про­из­вод­ной име­ет боль­шие зна­че­ния в об­ла­сти вы­со­ких ча­стот по срав­не­нию с мо­ду­лем ис­ход­но­го сиг­на­ла.