Практическая ширина спектра сигнала

Ре­аль­ные сиг­на­лы все­гда огра­ни­че­ны во вре­ме­ни, сле­до­ва­тель­но, их ам­пли­туд­ный спектр тео­ре­ти­че­ски не­огра­ни­чен. Од­на­ко ре­аль­ные сиг­на­лы ге­не­ри­ру­ют­ся и пе­ре­да­ют­ся устрой­ства­ми, со­дер­жа­щи­ми инер­ци­он­ные эле­мен­ты (на­при­мер, ём­ко­сти и ин­дук­тив­но­сти в элек­три­че­ских це­пях и про­чих пре­об­ра­зо­ва­те­лях). По­это­му они не мо­гут со­дер­жать гар­мо­ни­че­ских со­став­ля­ю­щих сколь угод­но вы­со­ких ча­стот.

В свя­зи с этим воз­ни­ка­ет не­об­хо­ди­мость вве­сти в рас­смот­ре­ние мо­де­ли сиг­на­лов, об­ла­да­ю­щих как ко­неч­ной дли­тель­но­стью, так и огра­ни­чен­ным спек­тром. При этом в со­от­вет­ствии с ка­ким-ли­бо кри­те­ри­ем до­пол­ни­тель­но огра­ни­чи­ва­ет­ся ли­бо ши­ри­на спек­тра, ли­бо дли­тель­ность сиг­на­ла, ли­бо оба па­ра­мет­ра од­но­вре­мен­но.

Ча­ще все­го в ка­че­стве та­ко­го кри­те­рия ис­поль­зу­ет­ся энер­ге­ти­че­ский кри­те­рий, со­глас­но ко­то­ро­му прак­ти­че­скую ши­ри­ну ам­пли­туд­но­го спек­тра Δω_пр вы­би­ра­ют так, что­бы в нём бы­ла со­сре­до­то­че­на по­дав­ля­ю­щая часть энер­гии сиг­на­ла. Для это­го ис­поль­зу­ют ра­вен­ство Пар­се­ва­ля, поз­во­ля­ю­щее опре­де­лить энер­гию сиг­на­ла E_c ли­бо че­рез функ­цию u(t), опи­сы­ва­ю­щую ре­аль­ный сиг­нал дли­тель­но­стью T_n, ли­бо че­рез мо­дуль её спек­траль­ной плот­но­сти |S(ω)|:

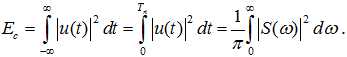
Прак­ти­че­ская ши­ри­на спек­тра сиг­на­ла, со­сре­до­то­чен­ная в диа­па­зо­не ча­стот от 0 до ω_гр не­ко­то­ро­го зна­че­ния , опре­де­ля­ет­ся из со­от­но­ше­ния:

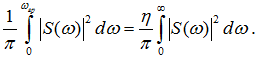
Здесь ω_гр — гра­нич­ная ча­сто­та, опре­де­ля­ю­щая верх­нее зна­че­ние спек­тра сиг­на­ла; η — ко­эф­фи­ци­ент, до­ста­точ­но близ­кий к 1 (на прак­ти­ке его зна­че­ние вы­би­ра­ют в ин­тер­ва­ле от 0,9 до 0,998 в за­ви­си­мо­сти от тре­бо­ва­ний к ка­че­ству вос­про­из­ве­де­ния сиг­на­ла). Зна­че­ние η = 0,99 озна­ча­ет, что в по­ло­се ча­стот от 0 до ω_пр со­дер­жит­ся 99 % энер­гии сиг­на­ла. Зна­че­ние гра­нич­ной ча­сто­ты на­хо­дят, ре­шая транс­цен­дент­ное урав­не­ние (5.15).