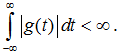Интеграл Дюамеля
Знание импульсной характеристики линейной стационарной системы позволяет получить фундаментальное соотношение, связывающее входной и выходной сигналы. Действительно, входной сигнал допускает представление вида:
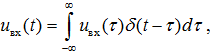
называемое фильтрующим свойством δ-функции. Отвечающая ему выходная реакция линейной стационарной системы запишется в виде:
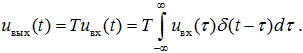
Так как интеграл представляет собой предельное значение суммы, линейный оператор T на основании принципа суперпозиции может быть внесён под знак интеграла. Учитывая, что оператор T воздействует лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ, получаем:
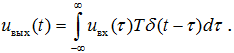
С учётом равенства (7.1) окончательно получаем интеграл Дюамеля:
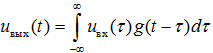
Соотношение (7.10) показывает, что выходной сигнал линейной стационарной системы представляет собой свёртку двух функций: входного сигнала и импульсной характеристики системы. Для реальных систем (физически реализуемых) всегда выполняется условие: g(t − τ) = 0 при t < τ, т. к. реакция такой системы (отклик на входное воздействие) не может опережать само входное воздействие. Следовательно, можно записать интеграл Дюамеля в виде:
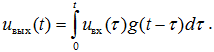
Таким образом, линейная стационарная система, выполняя обработку поступающего на вход сигнала, проводит в момент времени t операцию взвешенного суммирования всех его мгновенных значений за все предыдущее время. Роль весовой функции выполняет при этом импульсная характеристика системы.
Физически реализуемая система должна быть, кроме того, устойчивой. Это означает, что её импульсная характеристика должна удовлетворять условию абсолютной интегрируемости: