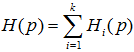Передаточная функция системы

Ре­ше­ние диф­фе­рен­ци­аль­но­го урав­не­ния ли­ней­ной си­сте­мы (6.4), свя­зы­ва­ю­ще­го вод­ные воз­дей­ствия и вы­ход­ные сиг­на­лы, мо­жет быть осу­ществ­ле­но опе­ра­тор­ным ме­то­дом с по­мо­щью ин­те­граль­но­го пре­об­ра­зо­ва­ния Ла­пла­са. При­мем до­пу­ще­ние, что u_вх(t) = 0 при t < 0. То­гда изоб­ра­же­ние по Ла­пла­су вход­но­го и вы­ход­но­го сиг­на­лов бу­дет иметь вид:

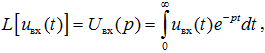
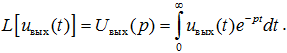
Вы­чис­лив пре­об­ра­зо­ва­ние Ла­пла­са от обе­их ча­стей урав­не­ния (6.4) с учё­том свой­ства 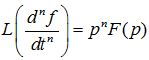, по­лу­чим:

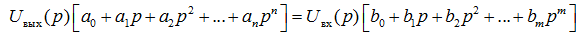
Вве­дём от­но­ше­ние изоб­ра­же­ний по Ла­пла­су вы­ход­но­го и вход­но­го сиг­на­лов, на­зы­ва­е­мое пе­ре­да­точ­ной функ­ци­ей или опе­ра­тор­ным ко­эф­фи­ци­ен­том пе­ре­да­чи си­сте­мы:

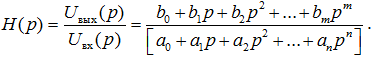
Ес­ли пе­ре­да­точ­ная функ­ция си­сте­мы из­вест­на, то по­иск вы­ход­ной ре­ак­ции си­сте­мы на за­дан­ное вход­ное воз­дей­ствие u_вх(t) раз­би­ва­ет­ся на три эта­па:

• u_вх(t) → U_вх(p);
• U_вых(p) = H(p)U_вх(p);
• U_вых(p) → u_вых(t);

Сиг­нал на вы­хо­де си­сте­мы u_вых(t) на­хо­дят с по­мо­щью об­рат­но­го пре­об­ра­зо­ва­ния Ла­пла­са:

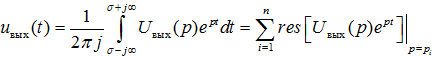
Как из­вест­но, спо­соб на­хож­де­ния ори­ги­на­ла вы­ход­но­го сиг­на­ла по его изоб­ра­же­нию с по­мо­щью тео­ре­мы о вы­че­тах без вы­чис­ле­ния ин­те­гра­ла ос­но­ван на пред­став­ле­нии подын­те­граль­но­го вы­ра­же­ния (7.17) в ви­де от­но­ше­ния двух мно­го­чле­нов φ(p)/ψ(p), опре­де­ле­нии по­лю­сов подын­те­граль­ной функ­ции (зна­че­ний p_i, яв­ля­ю­щих­ся кор­ня­ми зна­ме­на­те­ля ψ(p)) и вы­чис­ле­нии u_вых(t) по сум­ме вы­че­тов φ(p)/ψ(p) в со­от­вет­ству­ю­щих по­лю­сах p_i:

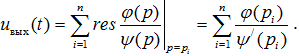
При опре­де­ле­нии пе­ре­да­точ­ных функ­ций слож­ных си­стем, со­сто­я­щих из ря­да от­дель­ных зве­ньев (пре­об­ра­зо­ва­те­лей, функ­ци­о­наль­ных бло­ков), вна­ча­ле опре­де­ля­ют пе­ре­да­точ­ные функ­ции от­дель­ных зве­ньев. Да­лее, ес­ли эти зве­нья со­еди­не­ны по­сле­до­ва­тель­но, опре­де­ля­ют об­щую пе­ре­да­точ­ную функ­цию си­сте­мы по фор­му­ле:

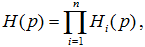
где H_i (p) — пе­ре­да­точ­ные функ­ции от­дель­ных зве­ньев (n — чис­ло зве­ньев).

Ес­ли k зве­ньев ка­кой ли­бо си­сте­мы со­еди­не­ны па­рал­лель­но, то рас­чёт ре­зуль­ти­ру­ю­щей пе­ре­да­точ­ной функ­ции этой ча­сти си­сте­мы осу­ществ­ля­ют по фор­му­ле: